In the world of information overload, ranking is paramount. Search engines need to rank webpages, e-commerce sites need to rank products, and recommendation systems need to rank suggested items. Simply retrieving relevant items isn't enough; presenting them in the best possible order is critical for user satisfaction and engagement.

This is the domain of Learning-to-Rank (LTR): using machine learning techniques to build models that predict the optimal ordering of items for a given query or user. While various approaches exist (pointwise, pairwise, listwise), one algorithm has consistently stood out for its robustness and effectiveness, especially in industrial settings: LambdaMART.

LambdaMART combines the power of gradient boosting trees (specifically MART - Multiple Additive Regression Trees) with a clever optimization technique derived from LambdaRank. It directly targets the optimization of ranking metrics like NDCG (Normalized Discounted Cumulative Gain), making it highly effective in practice.

This post dives deep into LambdaMART with the following topics:

• The challenge of optimizing ranking metrics.
• The journey from RankNet to LambdaRank to LambdaMART.
• How LambdaMART works conceptually.
• Its key components, advantages, and limitations.
• Its place among other LTR techniques, including deep learning.
• Where it's commonly applied.

Let's unravel the mechanics behind this ranking powerhouse.

The Challenge: Why Ranking is Different

Traditional machine learning often focuses on:

• Pointwise Regression/Classification: Predicting a value or class for a single item (e.g., predicting the CTR of one ad).
• Pairwise Classification: Predicting the relative order of two items (e.g., predicting if document A is more relevant than document B).

However, ranking quality is typically measured by listwise metrics like NDCG, MAP (Mean Average Precision), or ERR (Expected Reciprocal Rank). These metrics evaluate the entire ranked list, considering the positions of relevant items. The problem is that these metrics are often non-continuous and non-differentiable, making them difficult to optimize directly with standard gradient-based methods.

The Evolutionary Path: RankNet -> LambdaRank -> LambdaMART

Understanding LambdaMART requires understanding its predecessors:

1. RankNet (2005):

• Approach: Pairwise. It trains a neural network (or other model) to predict the relative relevance score for pairs of documents.
• Mechanism: For a given query, it considers pairs of documents (A, B). If A is truly more relevant than B, the model should output a higher score for A. It uses a probabilistic cost function (cross-entropy) based on the predicted score difference and the true relevance difference.
• Limitation: The cost function optimized (pairwise accuracy) doesn't perfectly correlate with listwise ranking metrics like NDCG. Optimizing pairwise accuracy might not lead to the best possible ranked list according to NDCG.

2. LambdaRank (2006 - Insight by Chris Burges):

• Approach: Still conceptually pairwise, but with a listwise goal.
• The "Aha!" Moment: LambdaRank realized you don't actually need the explicit RankNet cost function to perform gradient descent style optimization. You only need the gradients of the cost function with respect to the model's scores.
• Lambda Gradients: LambdaRank defined these gradients, called "lambdas" (λ). For a pair of documents (i, j) with scores (s_i, s_j), the lambda associated with document i due to this pair is calculated based on the sigmoid of the score difference (σ(s_i - s_j)). Crucially, this gradient is then multiplied by the change (Δ) in the target ranking metric (e.g., NDCG) that would occur if documents i and j were swapped in the current ranking.
• Interpretation: The magnitude of the "push" or "pull" applied to a document's score during training depends not just on the pairwise error but also on how much that swap impacts the overall listwise metric. It focuses the optimization effort where it matters most for the ranking metric.
• Limitation: LambdaRank was more of a concept for computing these special gradients; it didn't specify the underlying model architecture (though often associated with neural nets initially).

3. LambdaMART (2007):

• Approach: Listwise (by optimizing metric via gradients) using a specific model type.
• The Combination: LambdaMART brilliantly combines the LambdaRank gradients (λ) with the MART (Multiple Additive Regression Trees) algorithm, which is a form of Gradient Boosting Decision Trees (GBDT).
• Mechanism: Gradient Boosting works by iteratively building weak learners (decision trees) that try to predict the residuals or gradients of the loss function from the previous iteration. In LambdaMART:
  
  • For each query/list, calculate the LambdaRank gradients (λ) for each document based on the current model's scores and the target metric (e.g., NDCG). These lambdas represent the "pseudo-residuals" or target gradients.
  • Train a regression tree to predict these lambdas based on the document features.
  • Add this new tree to the ensemble model (with a learning rate).
  • Repeat for many iterations.

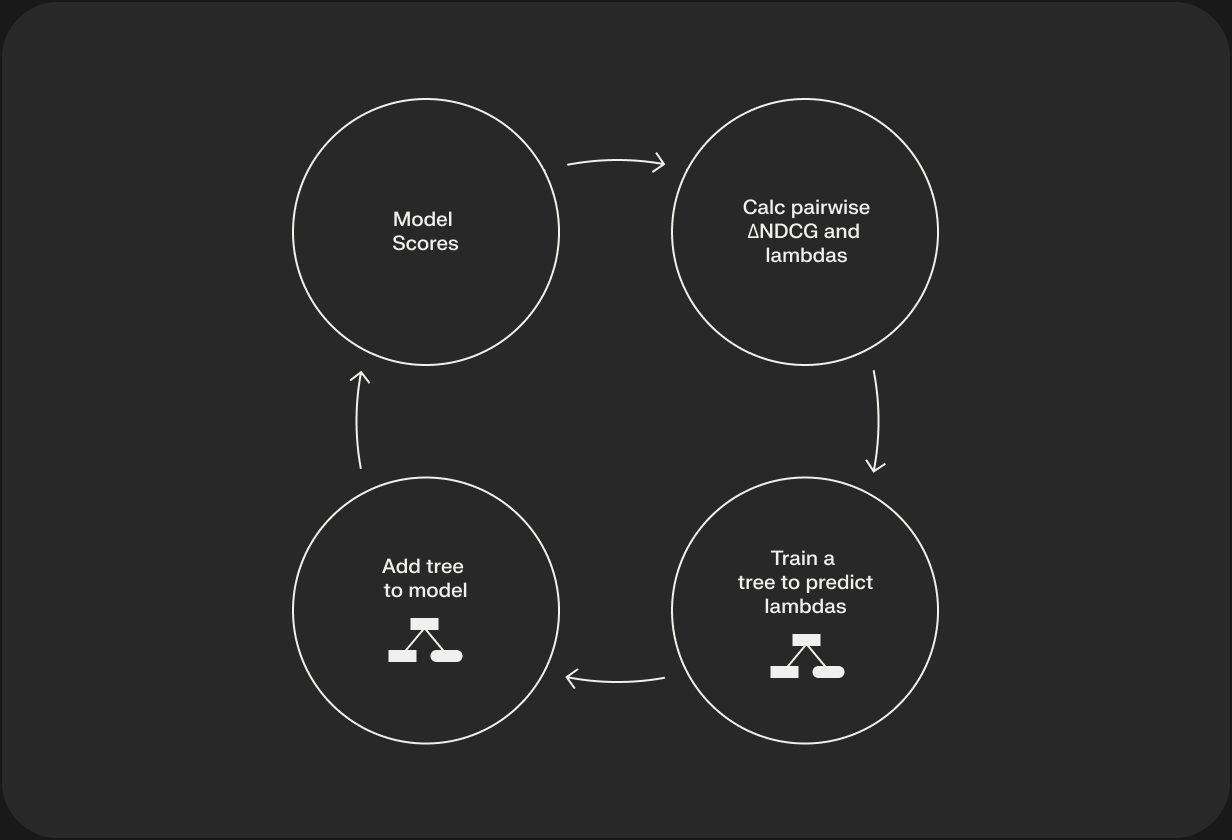
LambdaMART essentially uses MART as the engine and LambdaRank's metric-aware gradients as the fuel, directly optimizing for listwise ranking quality.

How LambdaMART Works: The Boosting Process

1. Initialization: Start with a constant prediction model (e.g., predicts 0 for all documents).
2. Iteration (Boosting Rounds): For m = 1 to M (number of trees):
   
   • Compute Lambdas: For each query (list of documents), use the current ensemble model (F_{m-1}) to predict scores for all documents. Calculate the LambdaRank gradients (λ) for each document, typically using NDCG as the target metric. These lambdas indicate how much each document's score needs to be adjusted (up or down) to improve the overall list's NDCG.
   • Fit a Regression Tree: Train a regression tree (h_m) using the document features as input and the computed lambdas (λ) as the target values. The tree learns patterns in features that correspond to needing a score adjustment.
   • Update Ensemble: Add the newly trained tree to the ensemble, usually scaled by a learning rate (ν): F_m(x) = F_{m-1}(x) + ν * h_m(x).
3. Final Model: The final model F_M(x) is the sum of all the trees, producing a relevance score for a given document x. Documents are then sorted by these scores to produce the final ranking.

Key Components and Considerations

• Features: LambdaMART works directly with feature vectors representing the query-document relationship (e.g., TF-IDF scores, BM25, URL length, PageRank, document age, click features). Feature engineering is crucial.
• Ranking Metric (for Lambdas): Choosing the metric to optimize (NDCG, MAP, ERR) is vital, as the lambdas depend on it. NDCG is very common. @K (e.g., NDCG@10) is often specified to focus on top-K positions.
• MART/GBDT Parameters: Standard gradient boosting parameters need tuning:
  
  • Number of trees (boosting rounds)
  • Learning rate (shrinkage)
  • Tree depth / Number of leaves
  • Subsampling rates (for data and features)
• Implementation: Widely available in popular libraries:
  
  • LightGBM: Highly efficient implementation, often preferred.
  • XGBoost: Another very popular and robust implementation.
  • RankLib: A Java library specifically for LTR algorithms.

Why Use LambdaMART? The Advantages

• ✅ Direct Metric Optimization: Its core strength – designed to directly optimize listwise ranking metrics like NDCG.
• ✅ State-of-the-Art Performance: For many years, it was (and often still is) considered the state-of-the-art or a very strong baseline for LTR on tabular feature data.
• ✅ Efficiency: Gradient Boosting Trees are generally fast at inference time compared to complex deep learning models.
• ✅ Robustness: Relatively robust to data noise and feature scaling (inherent in tree-based methods).
• ✅ Interpretability (Relative): Tree-based models offer some level of interpretability through feature importance scores (though ensembles are less interpretable than single trees).

Limitations and Disadvantages

• ❌ Training Complexity: Calculating pairwise lambda gradients can be computationally intensive during training, especially with long lists.
• ❌ Feature Engineering: Relies heavily on manually crafted features. Unlike deep learning, it cannot easily learn representations from raw inputs (like text or image pixels).
• ❌ Hyperparameter Sensitivity: Performance can be sensitive to the GBDT hyperparameters and the choice of ranking metric.
• ❌ No End-to-End Feature Learning: Cannot learn feature representations from raw data like deep models.

LambdaMART vs. Other Ranking Approaches

• Pointwise/Pairwise Methods (Logistic Regression, RankSVM): LambdaMART generally outperforms these as it directly targets listwise metrics.
• Other Listwise Methods (ListNet, ListMLE, AdaRank): These are alternative listwise approaches, each with pros and cons. LambdaMART often achieves a good balance of performance and efficiency.
• Deep Learning Rankers (DNNs, BERT-based, etc.):
  
  • Pros of DL: Can learn complex feature interactions and representations directly from raw or semi-structured data (text, logs, images), potentially achieving higher accuracy. More flexible architecture.
  • Cons of DL: Often slower inference, require more data, harder to train and tune, less interpretable.
  • Coexistence: LambdaMART is often used as a strong baseline. Sometimes deep models are used for feature extraction, and LambdaMART is used on top of these learned features. In some systems, LambdaMART might be used for an initial ranking stage, followed by a complex DL re-ranker.

Applications: Where is LambdaMART Used?

LambdaMART is a workhorse in many ranking scenarios:

• Web Search Ranking: A core component in major search engines for ranking organic results.
• E-commerce Search: Ranking products based on relevance, popularity, and business metrics.
• Recommendation System Ranking: Often used as the Ranker (Stage 2) in multi-stage recommendation systems, taking candidates from a retrieval stage (like a two-tower model) and re-ranking them based on rich features.
• Advertising Ranking: Determining the order of ads shown to users.
• Question Answering / Answer Ranking: Ranking potential answers to a query.

Challenges and Future Directions

While mature, research related to LambdaMART and GBDT-based ranking continues:

• Scalability: Further improving training efficiency on massive datasets.
• Online Learning: Adapting LambdaMART for real-time updates as new data arrives.
• Integrating Deep Features: Combining the strengths of GBDT ranking with features learned by deep models.
• Multi-Objective Ranking: Optimizing for multiple metrics simultaneously (e.g., relevance and diversity).
• Interpretability: Enhancing the interpretability of complex LambdaMART ensembles.

LambdaMART in Practice: An Example with Shaped

Platforms like Shaped streamline the use of sophisticated ranking models like LambdaMART. Since LambdaMART is often implemented using gradient boosting frameworks like LightGBM or XGBoost, you can configure these directly within Shaped's policy system, specifically targeting ranking objectives.

Here's how you might configure a LightGBM model to act as a LambdaMART ranker (scoring policy) in Shaped, optimizing for NDCG:

model:
  name: my-lambdamart-ranker
  policy_configs:
    scoring_policy:
      policy_type: lightgbm
      objective: lambdarank
      n_estimators: 1000
      max_depth: 8
      num_leaves: 31
      learning_rate: 0.05
      colsample_bytree: 0.8
      subsample: 0.8
    embedding_policy:
      policy_type: two-tower
      # ... other embedding policy configurations ...

In this example:

• We define a scoring_policy using lightgbm.
  

• Crucially, we set the objective to lambdarank. This tells LightGBM to use the LambdaRank gradients, effectively implementing the LambdaMART algorithm.
  

• We configure standard GBDT parameters like n_estimators, max_depth, num_leaves, learning_rate, etc., which would typically be tuned based on your specific data.
  

• This scoring policy would typically operate on candidate items retrieved by an embedding_policy (like the two-tower model shown here).

Using a platform like Shaped allows you to leverage the power of LambdaMART for optimizing ranking metrics without the need to manage the intricate details of gradient calculation and tree building yourself.

Conclusion: A Cornerstone of Learning-to-Rank

LambdaMART stands as a testament to the power of combining clever theoretical insights (LambdaRank's metric-aware gradients) with robust machine learning techniques (Gradient Boosting). Its ability to directly optimize non-differentiable ranking metrics like NDCG propelled it to become a dominant force in Learning-to-Rank for many years.

While deep learning offers new possibilities for feature representation and interaction modeling, LambdaMART remains a highly effective, efficient, and widely deployed algorithm, particularly when working with well-engineered feature sets. It serves as a crucial component in countless search and recommendation systems and remains a formidable baseline for any new ranking algorithm to beat. Understanding LambdaMART is essential for anyone serious about building effective ranking systems.

Further Reading / References

• Burges, C. J. C. (2010). From RankNet to LambdaRank to LambdaMART: An Overview. Microsoft Research Technical Report. (The definitive overview)
• Wu, Q., Burges, C. J., Svore, K. M., & Gao, J. (2008). Adapting boosting for information retrieval measures. Information Retrieval. (Early LambdaMART paper)
• Check documentation for LightGBM, XGBoost, and RankLib for implementation details.